One area I work in is image processing. Image processing in itself is a large topic: in addition to the usual classification problems, my colleagues and I are working on image segmentation, among other things.
If you would like to learn more about image segmentation, you can find an introduction on my course at the Heise Academy. The goal of this blog post is not to actually explain quantum theory or quantum computing. The internet is full of very good texts, images, and video tutorials about these topics. In fact, I just wanted to see if quantum computing could help me accelerate our AI – outlining what I’ve encountered.
What are quantum computers?
Quantum computers are initially reminiscent of the seventies and eighties, when computers took up entire rooms. The miniaturization that has taken place since then has probably amazed everyone – and continues to do so. Inevitably, I am reminded of the legendary statement from Thomas Watson, head of IBM at the time. He is reported to have said: “I think there is a world market for maybe five computers.”
Ten years ago, there was a similar feeling about quantum computers. However, miniaturization can clearly be seen here as well. This is very closely related to the way quantum computers are operated: most quantum computers require their components to be cooled to a temperature near absolute zero. Current research has managed to work with new materials and to achieve the functionality of certain computing elements at room temperature (info about this can be found here).
To understand quantum computing, you should at least have heard the following four terms before: qubits, superposition, entanglement, and tunneling. In a classical computer, all information is represented as bits.
Power – no power. Yes – no. One – Zero.
In a quantum computer, the information is represented as qubits. Zero, one, or any value in between. The arbitrary values in between only exist for a certain duration. For this duration, there is no decision whether the value of the qubit is 0 or 1. The value is then, as it were, in a superposition. It is only by measuring, that the superposition is resolved and “decided” whether the qubit takes the value 0 or 1. Thus, the act of measuring forces the qubit to decide on a value. Not only is this very strange, it still doesn’t add any speed to the system. Let’s keep looking.
Another important feature is the entanglement of qubits. One can store two classical bits in a pair of entangled qubits in such a way that it is possible to arbitrarily change the value of both bits independently by manipulating only one qubit. This is not at all intuitive. Let’s take a closer look. If one measures a qubit that is entangled with other qubits, then all entangled qubits change instantaneously with it. If one assumes that nothing in the universe can move faster than the speed of light, then by that reasoning, this should not work. This so-called ‘spooky action at a distance’ is not easily comprehended at first: force a qubit to choose a state and immediately the corresponding result can be measured at all ends of the “qubit system” without the time it would take for information to spread. Because it doesn’t matter in this case whether you only measure the system in a small laboratory or distributed over the entire planet.
The fact that nothing can travel faster than light is discussed in this interesting video: Why can’t you go faster than light?
Let’s try to make it clearer with a metaphor: Alice and Bob each get a sealed package with a colored ball inside it. They don’t know what color the ball is, but they do know that the balls in both packets are the same color. Here, the uncertainty as to which color a ball is represents the superposition; there are different states (colors) and only by measuring (opening the package) are these found out (determined). The information “both balls have the same color” is the entanglement in this example. Now when Alice opens her package, she immediately also knows what color Bob’s ball is.
As with any metaphor or analogy, there are inconsistencies between the original and the metaphor. The mistake here is that the result is not initially determined by the measurement. If there were a sort of magical sphere that only took on its color once the package was actually opened, the metaphor would be precise.
Another problem is that the measurement of quantum systems is not so clearly defined. It usually takes several measurements before the result is secured. This, in turn, is related to the fragility of quantum systems. Shocks, magnetic radiation, and even cosmic background radiation can affect the results of quantum computers.
Let’s move on to the fourth component of quantum computing, tunneling. In image processing with AI and especially with neural networks, the goal is often to minimize the errors that a neural network makes during training. For this, one applies the input (usually an image) to the neural network and observes the output. Let’s say we want to create images of handwritten digits 0-9 and get the corresponding number as output. Let’s also say that we have 1000 different images as input and we tell the network after each creation if it gave the right output. If not, training must continue. This means that the weightings are specifically changed so that for the next image, the network is marginally better. To do this, one uses an error function that compares the actual output with the desired output.
The optimization procedure, in which the minimum of the error curve is sought, is often likened to a person standing on a mountain at night with a lantern and wanting to descend as far as possible into the valley. They only see one step at a time and always move in the direction that gives them the steepest descent. In the process, they could well end up in a side valley that is not the deepest at all. However, climbing up again is too difficult and so the person stays in the side valley. This is suboptimal.
The tunneling of the quantum machines proceeds quite differently. It starts drilling tunnels through the mountains and very quickly finds the deepest part of the mountains. An introduction to this topic can also be found here.
So, we know that quantum computers are getting smaller and smaller, no longer need to be cooled to absolute zero under all circumstances, are sensitive, operate with 0, 1, and a superposition of qubits, and with entanglement. But how does that help me with my AI tasks?
Who has the most qubits?
At first, I thought that a quantum computer has as many qubits as a classical computer has bits. Wrong! The manufacturers of quantum computers are in real competition to see who can combine the most qubits, as error-free as possible, into quantum systems and keep them stable for as long as possible. Here we are talking about a few seconds.
So how many qubits are we talking about? Google has brought the concept of quantum supremacy into play. Quantum supremacy is called the point in time at which a quantum computer can solve a mathematical problem in a reasonable amount of time, that would take a classical computer years. However, quantum supremacy is defined independently of the usefulness of the solution. Therefore, it’s not about meaningful tasks, such as logistics, but rather academic tasks.
The hope of the industry, or in this case IBM, for the further development of qubits looks something like this:
But there are quite a few other players in this game, such as Microsoft, Amazon, Honeywell, Rigetti, and DWave. The number of companies that have quantum computers is also growing steadily. Only these are mentioned here: BASF, BMW, Bosch, Infineon, and Trumpf. And what is happening in the rest of the world at the same time? Here is an interesting article about this.
Although there is not yet a universally accepted measure of quantum computer performance, the first algorithms for quantum computers do exist. One of the most pioneering is that of Peter Shor. As early as 1994, the mathematician showed that an asymmetric encryption method can be solved in a reasonable amount of time using just a few qubits. This method is based on the fact that it is much easier to multiply large prime numbers than to factorize the result again. This is also called a one-way function. Shor proved that quantum computers can master this factorization very quickly. Shor’s algorithm was the first quantum algorithm that not only solved a truly practical problem but was also shown to produce results exponentially faster than the best-known algorithm for conventional computers to date. However, one must not consider qubits individually either. It is always about whole qubit systems with a quantum correlation. After the quantum systems have been entangled with each other, they should be seen as a single system.
I would like to emphasize that among companies, a competition of quantum computing systems is going on, leading to more and more quanta with greater and greater stability in smaller and smaller spaces. Also, not all quantum computers need to be severely cooled, which improves the economics of the systems. But can I even use such a computer as a “normal” IT consultant? Let’s wait and see.
How can I use quantum computers?
Can I use a quantum computer as a “normal” IT consultant? Yes and no. Or maybe? An initial search reveals that Google offers a framework, or rather a library, called Cirq and IBM one called Quiskit. If you look a little further, you can also find something under Microsoft Azure, and Amazon with Braket. So where to start?
I got started with the book Quantum Machine Learning with Python: Using Cirq from Google Research and IBM Qiskit by Pattanayak Santanu. Chapter 5 made me particularly curious (Quantum Machine Learning) and chapter 6 (Quantum Deep Learning), even more so. I looked at the sample code and took my first steps toward quantum computing. I was able to run and modify the examples from Google directly in Colab.
What a wonderful present! There are even examples that CNNs process. The book drew my attention to the relevant library: https://www.tensorflow.org/quantum. A great start! A first QCNN was quickly written. There are other examples and even the “Hello World” of AI. MNIST is available as a quantum version: https://www.tensorflow.org/quantum/tutorials/mnist. And the following program is really cool. https://www.tensorflow.org/quantum/tutorials/qcnn A true quantum CNN.
Have I reached my goal yet? Unfortunately not. What is very sobering, the examples are not really running on quantum computers at all, but are simulated! The companies offer their frameworks, so to speak, so that you can learn in advance how to program in the future. If you’re lucky enough to work at a research center where there are real quantum computers, you might even be able to use the coding. Or put another way: the people who write the frameworks already offer the code to the programming community. Actually, a fine move. Still, disappointing for me at first, since I will most likely not be able to work with it for the next few years.
But the first program, no longer called “Hello World” but characteristically, “Hello, Many Worlds,” explains everything needed to get started programming with quantum computershttps://www.tensorflow.org/quantum/tutorials/hello_many_worlds. Thanks, Google!
Slightly deflated, I wanted to know more and bought this book: Dancing with Qubits: How quantum computing works and how it can change the world by Robert S. Sutor. Here, the background is dealt with to a much greater degree. For a deeper start, you definitely need a healthy foundation in algebra, and in particular, you should be familiar with complex numbers.
But I actually wanted to run a program on a quantum computer to see how it solved my image recognition problems in a thousandth of a second. A friend pointed me in the right direction. Two types of quantum computers are currently in widespread use.Quantum annealing machines, which specialize in optimization tasks, and general-purpose quantum gate computers, which can, in principle, perform arbitrary computations. In both cases, programming is quite different from the way classical computers are programmed. The huge advantage of quantum annealing machines is that you can use them “for real”. Here and now.
Quantum computers are expensive and fickle
Arineo is doing very well. Can’t we just buy a quantum computer? This dream is over as quickly as a qubit can blink. This is a Berliner Morgenpost headline: Two billion euros for quantum computers “Made in Germany”. With this, the topic of universal quantum gate computers was settled for me for the time being.
A bird in the hand is worth two in the bush
A decision had already been made for me. If I can solve all kinds of problems super fast with universal quantum gate computers, but such a quantum gate computer is not really available to me, then I need another solution. The company Dwave advertises quantum computers with a so-called annealing process as a cloud service. The only limitation of the annealing method is that one can only solve certain optimization problems. Doesn’t matter for now, I just wanted to know more details. Here’s how to get started: https://www.dwavesys.com/
You can find masses of applications from well-known industrial companies with real problems that are common knowledge. For example, the Traveling Salesman Problem. We tested our first neural networks on this problem back in 1997 using Turbo Pascal. So how does this annealing process work? The answer can be found here. That convinced me at first. I register and can get started.
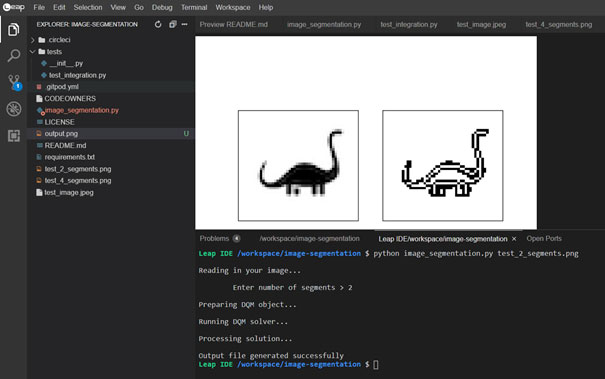
First, I look at the existing examples under “Explore our examples” and find an example for image segmentation under the keyword “Machine Learning”. In Dwave’s own IDE “leap”. Initially, I find mostly standard Python here, but also the LeapHybridDQMSampler. This is where I suspect the magic is.
from dwave.system import LeapHybridDQMSampler
You can learn more about it in these examples:
With a rough idea of how the solver works, I start the first program – a black and white image with only 2 segments. Is that Nessy?
Here is the call:
python image_segmentation.py test_2_segments.png
Here are the results:
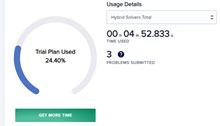
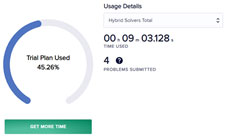
Preparing the DQM object takes about 1 minute and the DQM solver runs for another 5 minutes. The dashboard gives me an overview of my used free time.
Here is the snapshot before the run (I had already made 3 attempts).
Here is the snapshot after the run:
A detailed look at the costs will definitely be interesting if I want to work more with Dwave. No matter what one thinks of this particular result – the program does what it is supposed to do. Now, you may argue that you don’t need quantum computers for this. That’s true, but you could have said that about the first computers in the early years of computer science.
The first steps towards image processing have been taken. On a quantum computer using annealing techniques. In the cloud. Wow!
Let’s look at another example. This time no segmentation, but a classification between bees and ants. You can get access to many more examples via PennyLane:
Quantencomputer und künstliche Intelligenz Again, you have to be aware of whether you have a simulator or a real quantum computer in front of you. And there is more. On Amazon, under the keyword “braket”, you can find a whole range of quantum computer providers that you can book by the minute:https://aws.amazon.com/de/braket/
Conclusion
My initial question was:can quantum computers assist in image recognition using AI? In principle, the answer is yes. Even if complete integration is still a long way off. But there are, besides the expensive and not yet readily available universal quantum gate computers, so-called quantum annealing machines, specialized for optimization tasks and available in the cloud. It is now necessary to see if AI image recognition problems can be formulated in such a way that they can be solved with quantum annealing machines. The first hybrid approaches work, as the PennyLane contribution shows. Summary: the future holds really exciting tasks for my team and me.